189. Rotate Array

Given an integer array nums, rotate the array to the right by k steps, where k is non-negative.

Example 1:

Input: nums = [1,2,3,4,5,6,7], k = 3

Output: [5,6,7,1,2,3,4]

Explanation:

rotate 1 steps to the right: [7,1,2,3,4,5,6]

rotate 2 steps to the right: [6,7,1,2,3,4,5]

rotate 3 steps to the right: [5,6,7,1,2,3,4]

Example 2:

Input: nums = [-1,-100,3,99], k = 2

Output: [3,99,-1,-100]

Explanation:

rotate 1 steps to the right: [99,-1,-100,3]

rotate 2 steps to the right: [3,99,-1,-100]

原题链接: https://leetcode.com/problems/rotate-array/description/

给定一个数组，将其旋转的意思是：将数组左端移出的元素补充到数组右端。我们希望编写一个函数rotate(arr,k,n)，传入数组arr，数组长度n，旋转元素个数k，就可以得到数组旋转后的结果。

假设原始数组是：

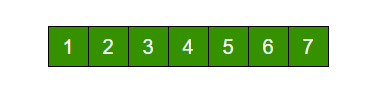
调用rotate(arr,2,7)后，就应该得到：

Juggling Algorithm

解决这个问题有很多种方法，下面要介绍的是一个名为“Juggling Algorithm”的算法。

它主要的思路分为 3 部分：

1. 将整个数组进行分为几个小组
2. 把小组内的每个元素向左移动 k 个位置
3. 处理下一个小组并重复第(2)步

具体来说，假设arr=[1,2,3,4,5,6], n=6, k=2，

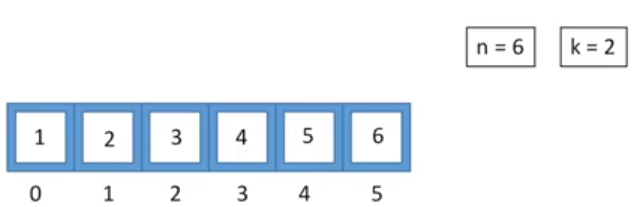
我们从index=0的元素开始处理（也就是 1），并把它的值存到变量temp中

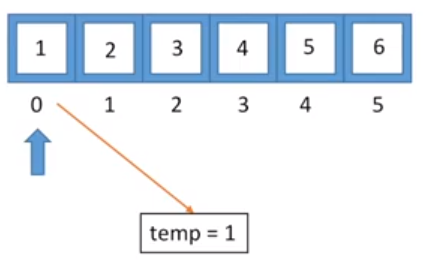
接下来，我们找到要把值移动到index=0的元素，其实就是index=2的元素，因为它距离index=0正好为 2（k=2）

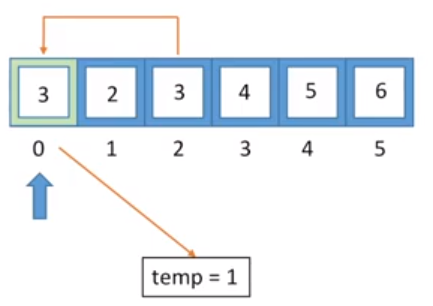
之后，我们把index=4的元素移动到index=2处

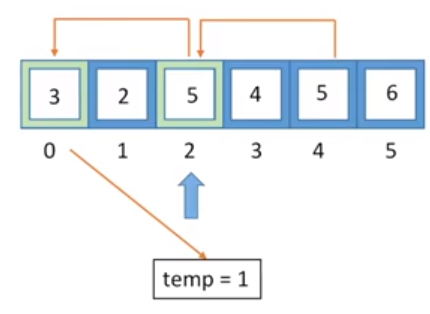
继续往后处理，此时我们应该处理index=4处的元素

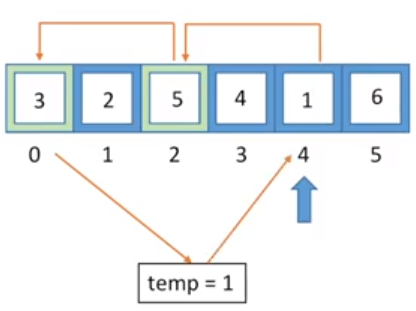
找到与它距离为 2 的元素，也就是index=0的元素，但这个元素一开始我们就处理过了，这标志着我们已经处理完了这个小组内的元素。 此时应该把存储在temp变量中的值赋给index=4的元素。

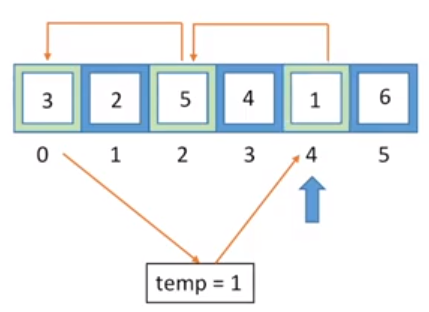
现在，我们知道了第一个小组内的元素下标为{0,2,4}。

接下来就是要按照思路(3)中谈到的，处理下一个小组，

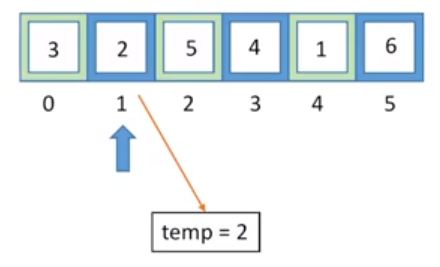
和处理第一个小组一样，我们可以类似处理好第二个小组

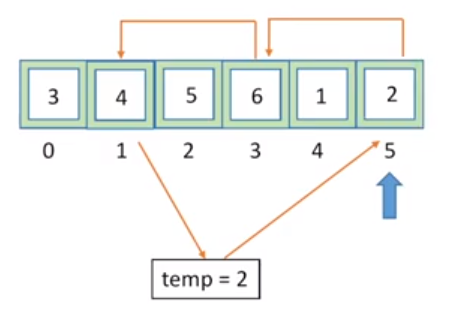
可以看到，整个处理过程包含两层循环：

• 外部循环用于遍历小组
• 内部循环用于将小组内的元素向左移动 k 个位置

那么问题来了：

1. 小组数是怎么确定的？
2. 小组内的元素怎么向左移动 k 个位置？
3. 什么时候处理下一个小组？

首先回答第 3 个问题 什么时候处理下一个小组? 根据上述的例子我们可以发现，当前处理小组的元素的下一个元素的下标如果等于小组的起始下标的时候，就意味着我们可以处理下一组了。

然后回答第 1 个问题 小组数是怎么确定的? 答案是GCD(n,k)，也就是n和k的最大公约数。这个结论是怎么得到的呢？根据第 3 个问题的回答，我们可以知道要处理到下一个小组(假设当前小组的起始下标为s)，经过的元素个数必然是n的倍数。拿上述的例子来说就是：当s=0 时，处理好当前小组进入下一个小组经过的元素为 6（$0 \to 2 \to 4 \to 0$）。当然，也可以重复这个过程，如$0 \to 2 \to 4 \to 0 \to 2 \to 4$。同时，我们也可以知道经过的元素个数必然是k的倍数。所以，经过的元素个数最少应该为LCM(n,k)，也就是n和k的最小公倍数。每一个小组包含的元素个数为：$\frac{LCM(n,k)}{k}$，那么，小组数应该为：

$$ \frac{n}{\frac{LCM(n,k)}{k}} = \frac{n * k}{LCM(n,k)} = GCD(n,k) $$

最后，为了回答第 2 个问题，我们看一个具体的例子，此时n=9,k=3

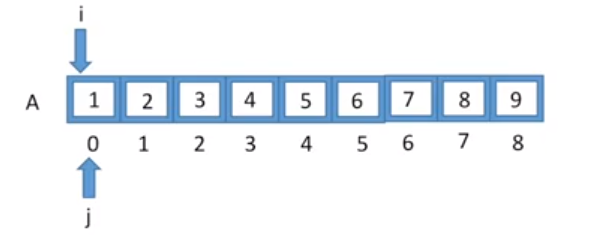
外部循环:i=0 to i < GCD(n,k) 内部循环:A[j]=A[(j+k)%n]，通过这样的方式向左移动 k 个位置。为了方便起见，可以让d=(j+k)%n。当d等于i时，处理下一组(也就是i自增 1)。

整个过程如下表所示：

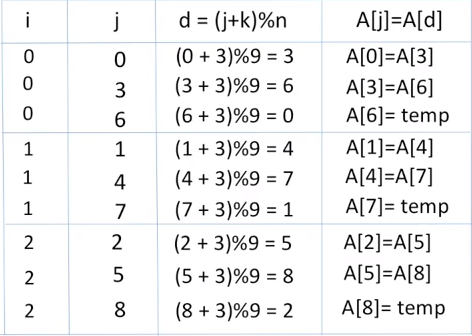
代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

def gcd(a, b):
    if b == 0:
        return a
    return gcd(b, a % b)

def rotate(arr, k, n):
    for i in range(gcd(k, n)):
        j = i
        temp = arr[i]
        while True:
            d = (j + k) % n
            if d == i:
                break
            arr[j] = arr[d]
            j = d
        arr[j] = temp

参考

• https://www.youtube.com/watch?v=utE_1ppU5DY
• https://www.geeksforgeeks.org/array-rotation/